Översikt över spatiala datatyper

Gäller för:SQL ServerAzure SQL DatabaseAzure SQL Managed InstanceSQL-analysslutpunkt i Microsoft FabricLager i Microsoft FabricSQL-databas i Förhandsversion av Microsoft Fabric

Det finns två typer av rumsliga data. Datatypen geometri stöder plan eller euklidisk (platt jord) data. geometri datatyp överensstämmer båda med Open Geospatial Consortium (OGC) Simple Features for SQL Specification version 1.1.0 och är kompatibel med SQL MM (ISO-standard).

SQL Server stöder också geografi datatyp, som lagrar ellipsoiddata (jorden runt), till exempel GPS-latitud och longitudkoordinater.

Rumsliga dataobjekt

geometri och geografi datatyper stöder 16 typer av rumsliga dataobjekt eller instanstyper. Men endast 11 av dessa instanstyper är instansierbara; du kan skapa och arbeta med dessa instanser (eller instansiera dem) i en databas. Dessa instanser härleder vissa egenskaper från sina överordnade datatyper.

Följande bild visar den geometrihierarki som geometri och geografi datatyper baseras på. De instansierbara typerna av geometri och geografi är angivna i blått.

Det finns ytterligare en instansierbar typ för datatypen geografi : FullGlobe. geometri och geografi typer kan känna igen en specifik instans så länge det är en välformulerad instans, även om instansen inte definieras explicit. Om du till exempel definierar en Point-instans explicit med hjälp av metoden STPointFromText() identifierar geometri och geografi instansen som en Point, så länge metodens indata är välformulerade. Om du definierar samma instans med hjälp av metoden STGeomFromText() identifierar både geometri och geografi datatyper instansen som en Point.

Undertyperna för geometri- och geografityper är indelade i enkla typer och samlingstyper. Vissa metoder som STNumCurves() fungerar bara med enkla typer.

Enkla typer är:

• Point
• LineString
• CircularString
• CompoundCurve
• Polygon
• CurvePolygon

Samlingstyper är:

• MultiPoint
• MultiLineString
• MultiPolygon
• GeometryCollection

Skillnader i datatyp för geometri och geografi

De två typerna av rumsliga data beter sig ofta på samma sätt. Det finns några viktiga skillnader i hur data lagras och manipuleras.

Så här definieras anslutningskanter

De definierande data för LineString-typen och Polygon-typen är endast hörn. Anslutningskanten mellan två hörn i en geometrityp är en rät linje. Anslutningskanten mellan två hörn i en geografityp är dock en kort storkretsbåge mellan de två hörnen. En stor ellips är skärningspunkten av ellipsoiden med ett plan genom dess centrum. En större elliptisk båge är ett bågsegment på den större ellipsen.

Så här definieras cirkulära bågsegment

Cirkulära bågsegment för geometrityper definieras på XY Cartesian-koordinatplanet (Z-värden ignoreras). Cirkulära bågsegment för geografityper definieras av kurvsegment på en referenssfär. Alla parallella på referenssfären kan definieras av två kompletterande cirkulära bågar där punkterna för båda bågarna har en konstant latitudvinkel.

Mätningar i rumsliga datatyper

I planarsystemet (flat-earth) ges mätningar av avstånd och områden i samma måttenhet som koordinater. Med hjälp av geometri datatyp är avståndet mellan (2, 2) och (5, 6) fem enheter, oavsett vilka enheter som används.

I ett ellipsoidalt eller jorden runt system ges koordinater i grader av latitud och longitud. Längder och områden mäts dock vanligtvis i meter och kvadratmeter, även om mätningen kan bero på den spatiala referensidentifieraren för geografi- instansen. Den vanligaste måttenheten för geografi datatyp är mätare.

Orientering av rumsliga data

Ringorienteringen för en polygon är inte en viktig faktor i planarsystemet. OGC Simple Features for SQL Specification anger inte en ringordning, och SQL Server har inte någon ringordning.

I ett ellipsoidsystem har en polygon utan orientering ingen betydelse eller är tvetydig. Beskriver till exempel en ring runt ekvatorn norra eller södra halvklotet? Om vi använder geografi datatyp för att lagra den rumsliga instansen måste vi ange ringens orientering och korrekt beskriva platsen för instansen.

Polygonens inre i ett ellipsoidsystem definieras av "vänsterregeln": om du föreställer dig att du går längs ringen i en geografi Polygon, följer punkterna i den ordning de listas, behandlas området till vänster som polygonens inre och området till höger som polygonens yttre.

När kompatibilitetsnivån är 100 eller lägre i SQL Server har geografi datatyp följande begränsningar:

• Varje geografi instans måste få plats på en enda halvklot. Inga rumsliga objekt som är större än en halvklot kan lagras.

• Alla geografiska områden instans från en Open Geospatial Consortium (OGC) Well-Known Text (WKT) eller Well-Known Binary (WKB) representation som producerar ett objekt som är större än en halvklot genererar en ArgumentException.

• De geografiska datatypsmetoder som kräver indata från två geografiska instanser, till exempel STIntersection(), STUnion(), STDifference()och STSymDifference(), returnerar null om resultaten från metoderna inte får plats på en enda halvklot. STBuffer() returnerar också null om utdata överstiger ett enda halvklot.

I SQL Server är FullGlobe en speciell typ av Polygon som täcker hela världen. Den har ett område, men inga kantlinjer eller hörn.

Yttre och inre ringar i datatypen geography

I OGC Simple Features for SQL Specification diskuteras yttre ringar och inre ringar, men den här skillnaden är föga meningsfull för SQL Server geografi- datatyp; någon ring av en polygon kan betraktas som den yttre ringen.

Mer information om OGC-specifikationer finns i följande dokument:

• OGC-specifikationer, enkel funktionsåtkomst del 1 – Gemensam arkitektur
• OGC-specifikationer, enkel funktionsåtkomst del 2 – SQL-alternativ

Cirkulära bågsegment

Tre instanserbara typer kan ta cirkulära bågsegment: CircularString, CompoundCurveoch CurvePolygon. Ett cirkulärt bågsegment definieras av tre punkter i ett tvådimensionellt plan och den tredje punkten kan inte vara samma som den första punkten. Några exempel på cirkulära bågsegment:

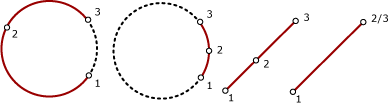
De första två exemplen visar typiska cirkulära bågsegment. Observera hur var och en av de tre punkterna ligger i en cirkels perimeter.

Andra två exempel visar hur ett linjesegment kan definieras som ett cirkulärt bågsegment. Tre punkter behövs fortfarande för att definiera det cirkulära arc-segmentet till skillnad från ett vanligt linjesegment, som bara kan definieras med två punkter.

Metoder som arbetar med cirkulära bågsegmenttyper använder raka segment för att approximera den cirkulära bågen. Antalet linjesegment som används för att approximera bågen beror på bågens längd och krökning. Z-värden kan lagras för var och en av de cirkulära arc-segmenttyperna, men används inte i beräkningarna.

Jämförelse mellan LineStr och CircularString

Det här exemplet visar hur du lagrar identiska isosceles trianglar med både en LineString-instans och CircularString-instans:

DECLARE @g1 geometry;
DECLARE @g2 geometry;
SET @g1 = geometry::STGeomFromText('LINESTRING(1 1, 5 1, 3 5, 1 1)', 0);
SET @g2 = geometry::STGeomFromText('CIRCULARSTRING(1 1, 3 1, 5 1, 4 3, 3 5, 2 3, 1 1)', 0);
IF @g1.STIsValid() = 1 AND @g2.STIsValid() = 1
  BEGIN
      SELECT @g1.ToString(), @g2.ToString()
      SELECT @g1.STLength() AS [LS Length], @g2.STLength() AS [CS Length]
  END

En CircularString--instans kräver sju punkter för att definiera triangeln. LineString instans kräver bara fyra punkter för att definiera triangeln. Anledningen till detta är att en CircularString- instans lagrar cirkulära bågsegment och inte linjesegment. Sidorna i triangeln som lagras i instansen CircularString är ABC, CDE och EFA. Sidorna i triangeln som lagras i instansen LineString är AC, CE och EA.

Tänk på följande exempel:

SET @g1 = geometry::STGeomFromText('LINESTRING(0 0, 2 2, 4 0)', 0);
SET @g2 = geometry::STGeomFromText('CIRCULARSTRING(0 0, 2 2, 4 0)', 0);
SELECT @g1.STLength() AS [LS Length], @g2.STLength() AS [CS Length];

Här är resultaten.

LS Length    CS Length
5.65685...   6.28318...

CircularString-instanser använder färre punkter för att lagra kurvgränser med större precision än LineString instanser. CircularString instanser är användbara för att lagra cirkulära gränser som en sökradie på 20 mil från en viss punkt. LineString instanser är bra för att lagra gränser som är linjära som ett fyrkantigt kvarter.

LineStr- och CompoundCurve-jämförelse

Följande kodexempel visar hur du lagrar samma bild med hjälp av LineString och CompoundCurve-instanser:

SET @g = geometry::Parse('LINESTRING(2 2, 4 2, 4 4, 2 4, 2 2)');
SET @g = geometry::Parse('COMPOUNDCURVE((2 2, 4 2), (4 2, 4 4), (4 4, 2 4), (2 4, 2 2))');
SET @g = geometry::Parse('COMPOUNDCURVE((2 2, 4 2, 4 4, 2 4, 2 2))');

I föregående exempel kan antingen en LineString--instans eller en CompoundCurve--instans lagra bilden. I nästa exempel används en CompoundCurve för att lagra en pajbit:

SET @g = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING(2 2, 1 3, 0 2),(0 2, 1 0, 2 2))');  

En CompoundCurve- instans kan lagra det cirkulära bågsegmentet (2 2, 1 3, 0 2) direkt, men en LineString- instans skulle behöva konvertera kurvan till flera mindre linjesegment.

Jämförelse av CircularStr och CompoundCurve

Följande kodexempel visar hur cirkelsegmentet kan lagras i en CircularString--instans:

DECLARE @g geometry;
SET @g = geometry::Parse('CIRCULARSTRING( 0 0, 1 2.1082, 3 6.3246, 0 7, -3 6.3246, -1 2.1082, 0 0)');
SELECT @g.ToString(), @g.STLength();

Att lagra cirkelsegmentet med hjälp av en CircularString-instans kräver att tre punkter används för varje linjesegment. Om en mellanliggande punkt inte är känd måste den antingen beräknas eller så måste slutpunkten för linjesegmentet fördubblas som följande kodfragment visar:

SET @g = geometry::Parse('CIRCULARSTRING( 0 0, 3 6.3246, 3 6.3246, 0 7, -3 6.3246, 0 0, 0 0)');

CompoundCurve instanser tillåter både LineString och CircularString komponenter så att endast två punkter till linjesegmenten i tårtbiten behöver anges. Det här kodexemplet visar hur du använder en CompoundCurve- för att lagra samma bild:

DECLARE @g geometry;
SET @g = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING( 3 6.3246, 0 7, -3 6.3246), (-3 6.3246, 0 0, 3 6.3246))');
SELECT @g.ToString(), @g.STLength();

Polygon- och CurvePolygon-jämförelse

CurvePolygon instanser kan använda CircularString och CompoundCurve instanser när de definierar sina yttre och inre ringar. polygoninstanser kan inte.

Limitations

I SQL-databasen i Förhandsversionen av Microsoft Fabric stöds datatyper för geografi och geometri , men de kan inte speglas i Fabric OneLake.

Relaterat innehåll

• Rumsliga data
• Referens för metod för geometri-datatyper
• metodreferens för geografidatatyp
• STNumCurves (geometridatatyp)
• STNumCurves (geografidatatyp)
• STGeomFromText (geometridatatyp)
• STGeomFromText (geografidatatyp)