Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
Your dataset is split into two parts: a set for training, and a set for testing. The training set is used to train the model, while the testing set is used as a test for model after training to calculate the model performance and evaluation. The testing set isn't introduced to the model through the training process, to make sure that the model is tested on new data.
Model evaluation is triggered automatically after training is completed successfully. The evaluation process starts by using the trained model to predict user defined entities for documents in the test set, and compares them with the provided data tags (which establishes a baseline of truth). The results are returned so you can review the model's performance. For evaluation, custom NER uses the following metrics:
Precision: Measures how precise/accurate your model is. It's the ratio between the correctly identified positives (true positives) and all identified positives. The precision metric reveals how many of the predicted entities are correctly labeled.
Precision = #True_Positive / (#True_Positive + #False_Positive)Recall: Measures the model's ability to predict actual positive classes. It's the ratio between the predicted true positives and what was tagged. The recall metric reveals how many of the predicted entities are correct.
Recall = #True_Positive / (#True_Positive + #False_Negatives)F1 score: The F1 score is a function used when you seek a balance between Precision and Recall.
F1 Score = 2 * Precision * Recall / (Precision + Recall)
Note
Precision, recall, and F1 score are calculated for each entity separately (entity-level evaluation) and for the model collectively (model-level evaluation).
Model-level and entity-level evaluation metrics
Precision, recall, and F1 score are calculated for each entity separately (entity-level evaluation) and for the model collectively (model-level evaluation).
The definitions of precision, recall, and evaluation are the same for both entity-level and model-level evaluations. However, the counts for True Positives, False Positives, and False Negatives differ can differ. For example, consider the following text.
Example
The first party of this contract is John Smith, resident of 5678 Main Rd., City of Frederick, state of Nebraska. And the second party is Forrest Ray, resident of 123-345 Integer Rd., City of Corona, state of New Mexico. There's also Fannie Thomas resident of 7890 River Road, city of Colorado Springs, State of Colorado.
The model extracting entities from this text could have the following predictions:
| Entity | Predicted as | Actual type |
|---|---|---|
| John Smith | Person | Person |
| Frederick | Person | City |
| Forrest | City | Person |
| Fannie Thomas | Person | Person |
| Colorado Springs | City | City |
Entity-level evaluation for the person entity
The model would have the following entity-level evaluation, for the person entity:
| Key | Count | Explanation |
|---|---|---|
| True Positive | 2 | John Smith and Fannie Thomas were correctly predicted as person. |
| False Positive | 1 | Frederick was incorrectly predicted as person while it should be city. |
| False Negative | 1 | Forrest was incorrectly predicted as city while it should be person. |
- Precision:
#True_Positive / (#True_Positive + #False_Positive)=2 / (2 + 1) = 0.67 - Recall:
#True_Positive / (#True_Positive + #False_Negatives)=2 / (2 + 1) = 0.67 - F1 Score:
2 * Precision * Recall / (Precision + Recall)=(2 * 0.67 * 0.67) / (0.67 + 0.67) = 0.67
Entity-level evaluation for the city entity
The model would have the following entity-level evaluation, for the city entity:
| Key | Count | Explanation |
|---|---|---|
| True Positive | 1 | Colorado Springs was correctly predicted as city. |
| False Positive | 1 | Forrest was incorrectly predicted as city while it should be person. |
| False Negative | 1 | Frederick was incorrectly predicted as person while it should be city. |
- Precision =
#True_Positive / (#True_Positive + #False_Positive)=1 / (1 + 1) = 0.5 - Recall =
#True_Positive / (#True_Positive + #False_Negatives)=1 / (1 + 1) = 0.5 - F1 Score =
2 * Precision * Recall / (Precision + Recall)=(2 * 0.5 * 0.5) / (0.5 + 0.5) = 0.5
Model-level evaluation for the collective model
The model would have the following evaluation for the model in its entirety:
| Key | Count | Explanation |
|---|---|---|
| True Positive | 3 | John Smith and Fannie Thomas were correctly predicted as person. Colorado Springs was correctly predicted as city. This number is the sum of true positives for all entities. |
| False Positive | 2 | Forrest was incorrectly predicted as city while it should be person. Frederick was incorrectly predicted as person while it should be city. This number is the sum of false positives for all entities. |
| False Negative | 2 | Forrest was incorrectly predicted as city while it should be person. Frederick was incorrectly predicted as person while it should be city. This number is the sum of false negatives for all entities. |
- Precision =
#True_Positive / (#True_Positive + #False_Positive)=3 / (3 + 2) = 0.6 - Recall =
#True_Positive / (#True_Positive + #False_Negatives)=3 / (3 + 2) = 0.6 - F1 Score =
2 * Precision * Recall / (Precision + Recall)=(2 * 0.6 * 0.6) / (0.6 + 0.6) = 0.6
Interpreting entity-level evaluation metrics
So what does it actually mean to have high precision or high recall for a certain entity?
| Recall | Precision | Interpretation |
|---|---|---|
| High | High | The model identified the entity. |
| Low | High | The model can't always extract this entity, but when it does it is with high confidence. |
| High | Low | The model extracts this entity well; however it is with low confidence as it is sometimes extracted as another type. |
| Low | Low | The model doesn't identify this entity type because it isn't normally extracted. When it is, it isn't with high confidence. |
Guidance
After you trained your model, you see some guidance and recommendation on how to improve the model. A model that covers all points in the guidance section is recommended.
Training set has enough data: When an entity type has fewer than 15 labeled examples in the training data, the model's accuracy drops. This result occurs because it lacks sufficient exposure to those cases. In this case, consider adding more labeled data in the training set. You can check the data distribution tab for more guidance.
All entity types are present in test set: When the testing data lacks labeled instances for an entity type, the model's test performance may become less comprehensive due to untested scenarios. You can check the test set data distribution tab for more guidance.
Entity types are balanced within training and test sets: When sampling bias causes an inaccurate representation of an entity type's frequency, it can lead to lower accuracy due to the model expecting that entity type to occur too often or too little. You can check the data distribution tab for more guidance.
Entity types are evenly distributed between training and test sets: When the mix of entity types doesn't match between training and test sets, it can lead to lower testing accuracy due to the model being trained differently from how it's being tested. You can check the data distribution tab for more guidance.
Unclear distinction between entity types in training set: When the training data is similar for multiple entity types, it can lead to lower accuracy because the entity types may be frequently misclassified as each other. Review the following entity types and consider merging them if they're similar. Otherwise, add more examples to better distinguish them from each other. You can check the confusion matrix tab for more guidance.
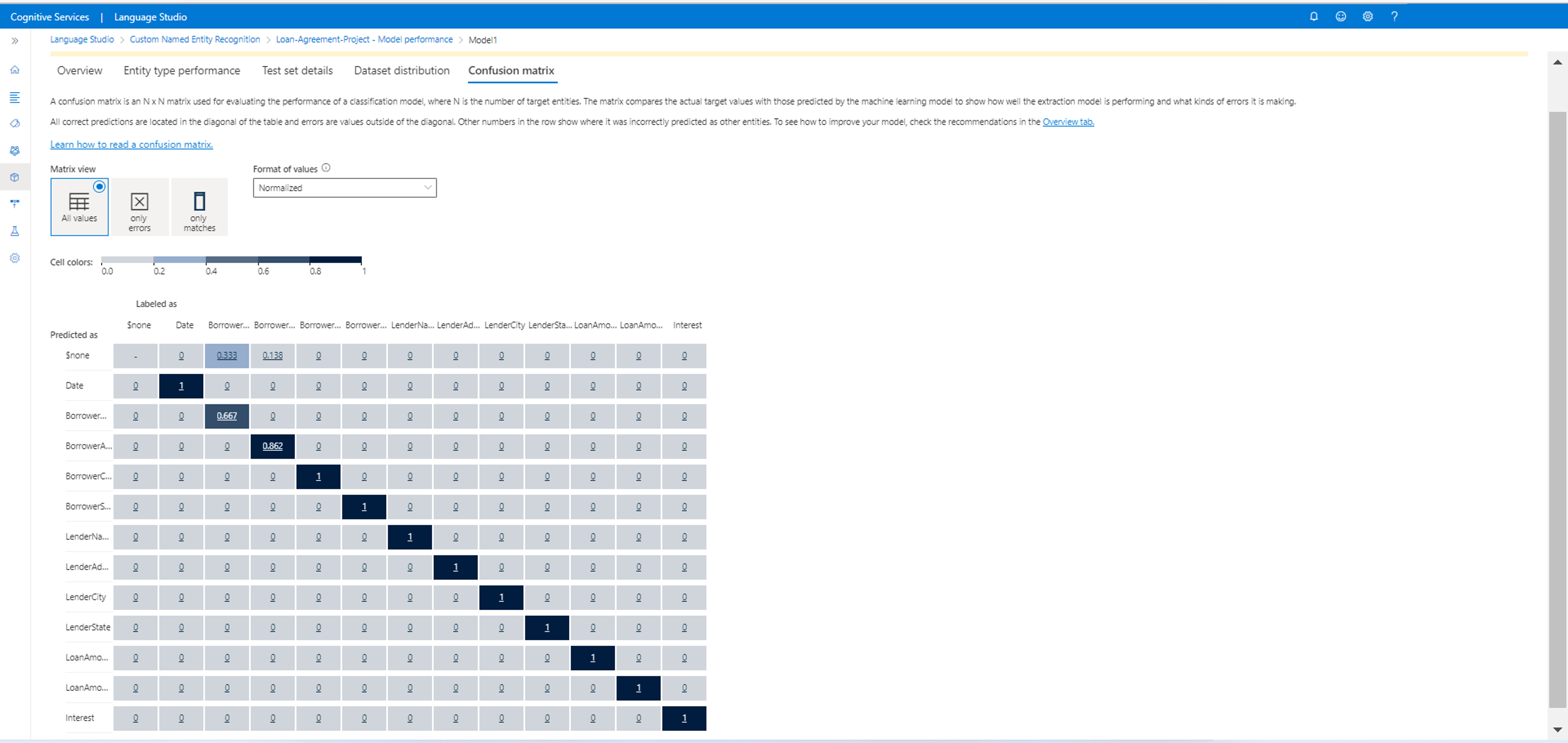
Confusion matrix
A Confusion matrix is an N x N matrix used for model performance evaluation, where N is the number of entities. The matrix compares the expected labels with the ones predicted by the model. This matrix gives a holistic view of how well the model is performing and what kinds of errors it's making.
You can use the Confusion matrix to identify entities that are too close to each other and often get mistaken (ambiguity). In this case consider merging these entity types together. If that isn't possible, consider adding more tagged examples of both entities to help the model differentiate between them.
The highlighted diagonal in the following image is the correctly predicted entities, where the predicted tag is the same as the actual tag.
You can calculate the entity-level and model-level evaluation metrics from the confusion matrix:
- The values in the diagonal are the True Positive values of each entity.
- The sum of the values in the entity rows (excluding the diagonal) is the false positive of the model.
- The sum of the values in the entity columns (excluding the diagonal) is the false Negative of the model.
Similarly,
- The true positive of the model is the sum of true Positives for all entities.
- The false positive of the model is the sum of false positives for all entities.
- The false Negative of the model is the sum of false negatives for all entities.